
This property stems directly from the Same Side Interior Angles Theorem, because any side of a parallelogram can be thought of as a transversal of two parallel sides. Whatever angle you choose, that angle and the angle next to it (in either direction) will sum to 180°. Here is parallelogram MATH: Consecutive angles in a parallelogram are supplementary Since the converse of the theorem tells us the interior angles will be supplementary if the lines are parallel, and we see that 145 ° − 35 ° = 180 ° 145°-35°=180° 145° − 35° = 180°, then the lines must be parallel.Ĭonsecutive Angles in a Parallelogram are Supplementary - One property of parallelograms is that their consecutive angles (angles next to each other, sharing a side) are supplementary.

Here are two lines and a transversal, with the measures for two same side interior angles shown: Same side interior angles theorem This is an especially useful theorem for proving lines are parallel. The converse theorem tells us that if a transversal intersects two lines and the interior angles on the same side of the transversal are supplementary, then the lines are parallel. The converse of the Same Side Interior Angles Theorem is also true. Same Side Interior Angles Theorem states that if a transversal intersects two parallel lines, then the interior angles on the same side of the transversal are supplementary.Ī transversal through two lines creates eight angles, four of which can be paired off as same side interior angles. Since either ∠ C \angle C ∠ C or ∠ A \angle A ∠ A can complete the equation, then ∠ C = ∠ A \angle C=\angle A ∠ C = ∠ A. We know two true statements from the theorem: Two theorems involve parallel lines.Ĭongruent Supplements Theorem says that If two angles - we'll call them ∠ C \angle C ∠ C and ∠ A \angle A ∠ A - are both supplementary to a third angle (we'll call it ∠ T \angle T ∠ T), then ∠ C \angle C ∠ C and ∠ A \angle A ∠ A are congruent. Supplementary angles are seen in three geometry theorems. The third set has three angles that sum to 180° three angles cannot be supplementary. Only those pairs are supplementary angles. Notice the only sets that sum to 180° are the first, fifth, sixth and eighth pairs. Identify the ones that are supplementary:
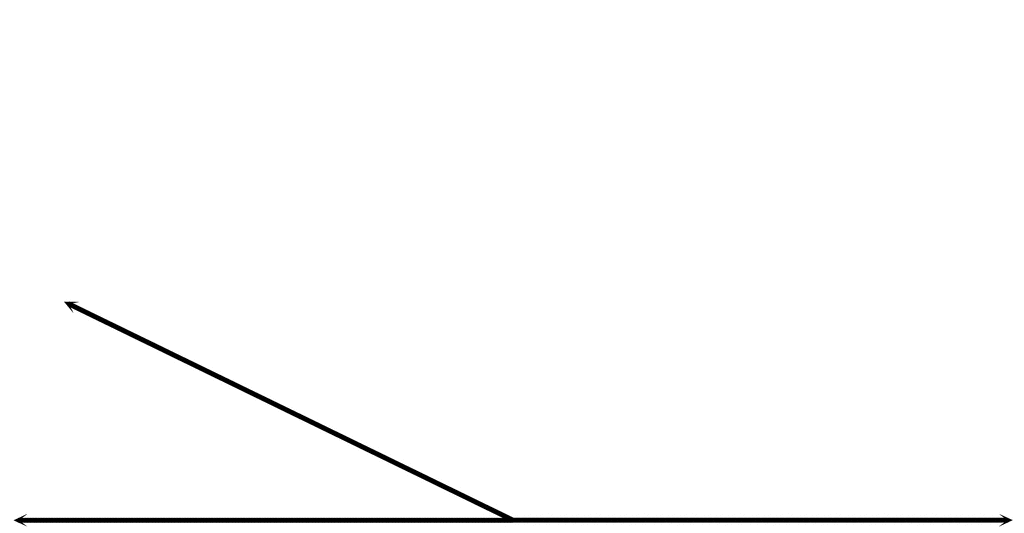

Here are eight sets of angles in degrees. The two angles must either both be right angles, or one must be an acute angle and the other an obtuse angle Only two angles can sum to 180°- three or more angles may sum to 180° or π \pi π radians, but they are not considered supplementary Supplementary angles have two properties: Straight angles - measuring exactly 180° or exactly π \pi π radians Types of supplementary angles Four angle typesĪcute angles - measuring less than 90° or less than π 2 \frac 2 π radians Supplementary angles can also have no common sides or common vertex. Supplementary angles can also share a common vertex but not share a common side. Supplementary angles sharing a common side will form a straight line. Supplementary angles are easy to see if they are paired together, sharing a common side.


 0 kommentar(er)
0 kommentar(er)
